Rob Siegwart - Change of Basis and the Transformation Matrix

A vector is represented traditionally with respect to a coordinate system. More generally it is represented by a set of basis vectors - two vectors which are linearly independent and form a vector subspace. A vector is therefore a linear combination of these basis vectors. In a global cartesian coordinate system these are the unit vectors \(\hat{x}\), \(\hat{y}\), and \(\hat{z}\). A vector can be represented in another coordinate system by changing its basis vectors.

Definitions

With:

\(M\), a basis matrix containing the basis vectors as columns
\(\vec{v}\), a column vector in the basis vector space \(M\)

When written as:

\begin{equation*} \vec{a} = M\vec{v} \end{equation*}

the vector \(\hat{a}\) is the vector in global coordinates.

The reverse can be achieved to determine a vector defined by a different basis:

\begin{equation*} \vec{v}=M^{-1}\vec{a} \end{equation*}

This works both for 2-D and 3-D vectors.

Example

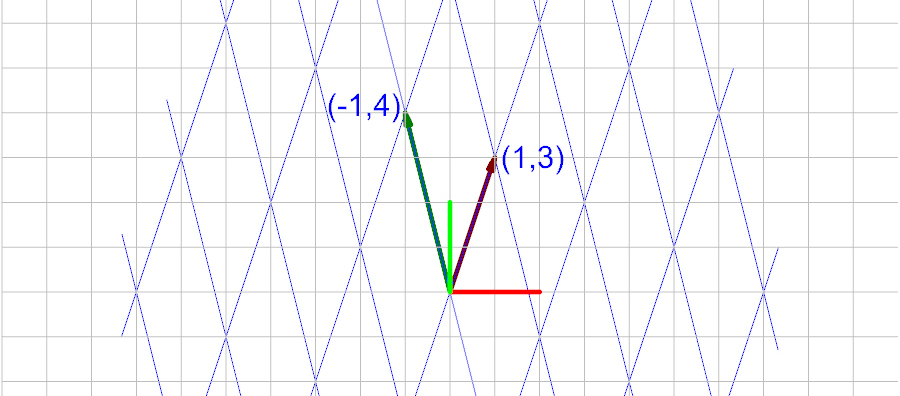
Let a set of basis vectors be defined as:

\begin{equation*} \begin{bmatrix}1&3\end{bmatrix} \end{equation*}

and

\begin{equation*} \begin{bmatrix}-1&4\end{bmatrix} \end{equation*}

The basis matrix being:

\begin{equation*} M=\begin{bmatrix}1&-1\\4&4\end{bmatrix} \end{equation*}

These basis vectors result in the following grid when plotted:

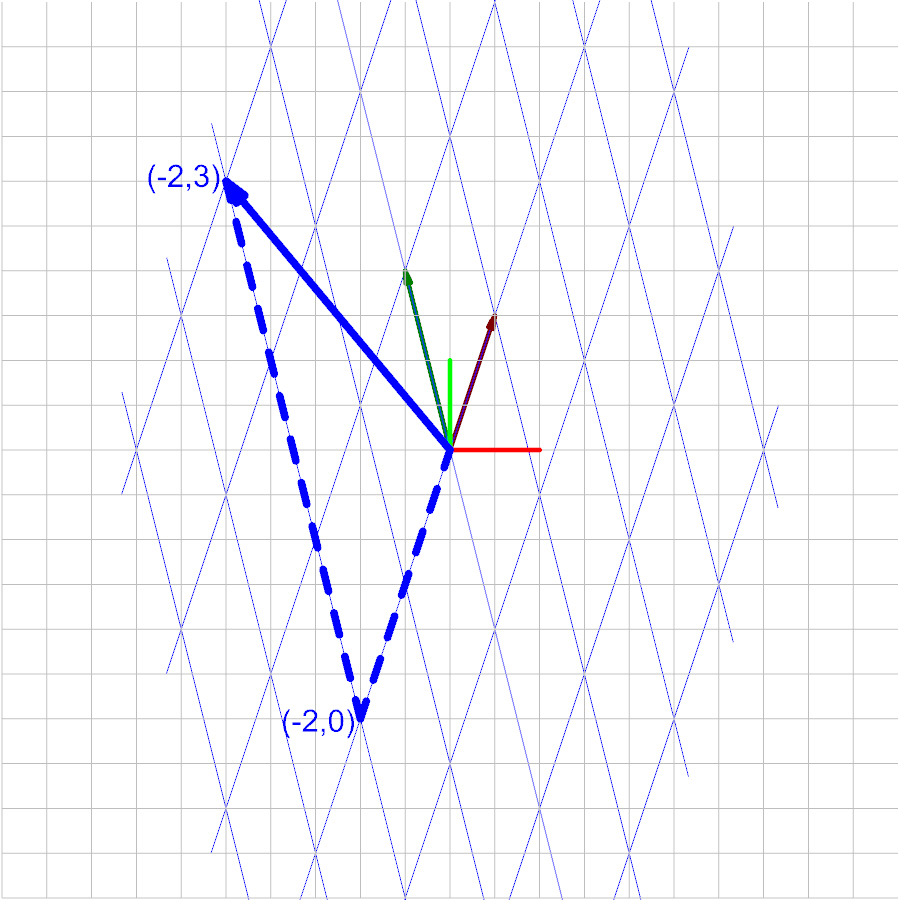
Conversion to Global Coordinates

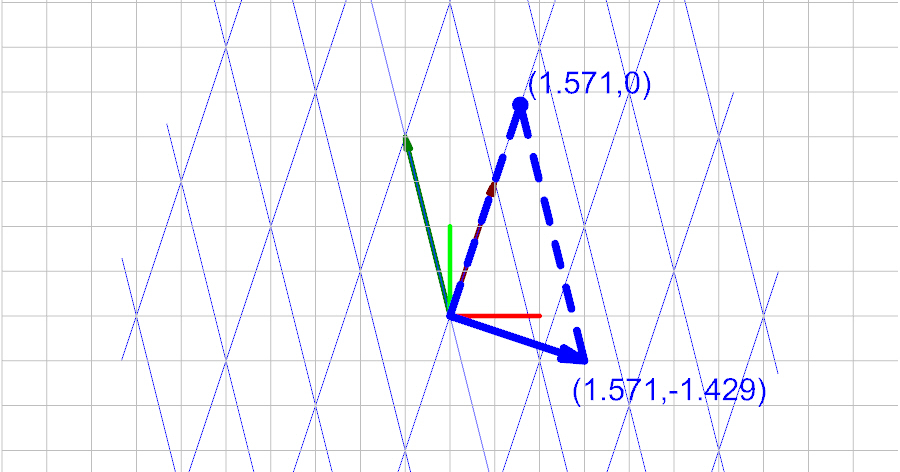
Set a vector in this space equal to \(\begin{bmatrix}-2&3\end{bmatrix}\).

This vector using basis coordinates is plotted as the following:

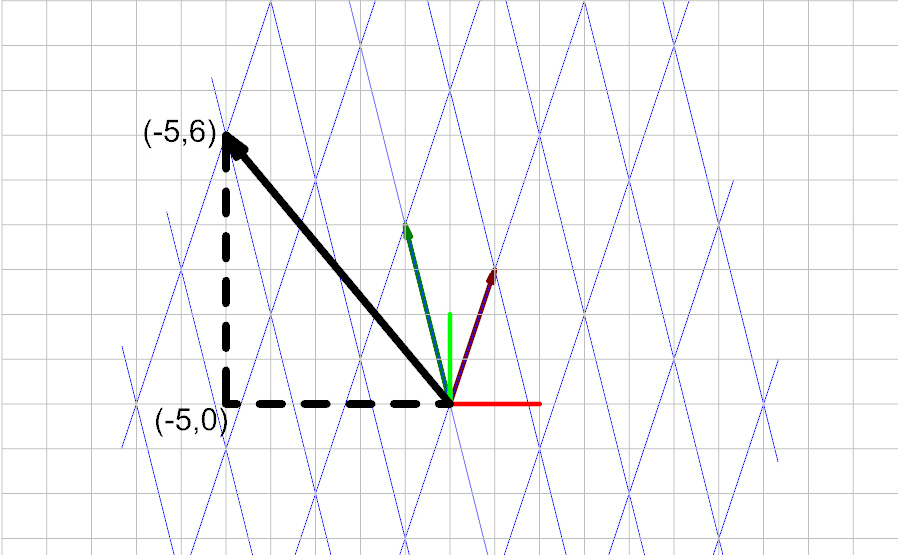
The vector \(\vec{a}\) (in global coordinates) is calculated with Eq 1. and is therefore equal to

\begin{equation*} \vec{a}=\begin{bmatrix}1&-1\\3&4\end{bmatrix}\begin{bmatrix}-2\\3\end{bmatrix}=\begin{bmatrix}-5&6\end{bmatrix} \end{equation*}

Converstion to Basis Coordinates

Using a vector in global coordinates of:

\begin{equation*} a=\begin{bmatrix}3&-1\end{bmatrix} \end{equation*}

we have:

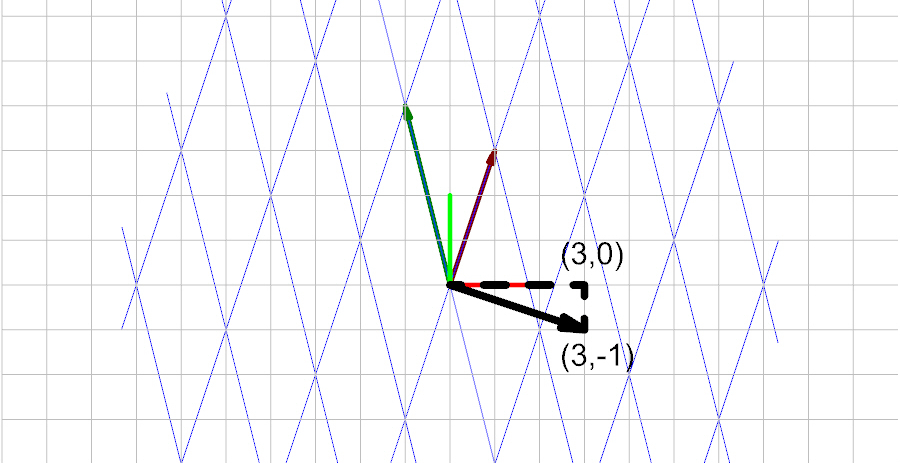
And to convert it to the basis space, we multiply the vector by the inverse of the basis matrix.

\begin{equation*} v=\begin{bmatrix}1&-1\\3&4\end{bmatrix}^{-1}\begin{bmatrix}3\\1\end{bmatrix}=\begin{bmatrix}0.571&0.143\\-0.429&0.143\end{bmatrix}\begin{bmatrix}3\\1\end{bmatrix}=\begin{bmatrix}1.571\\-1.429\end{bmatrix} \end{equation*}

Transformation Matrix

Change of basis can be used to derive transformation matices.

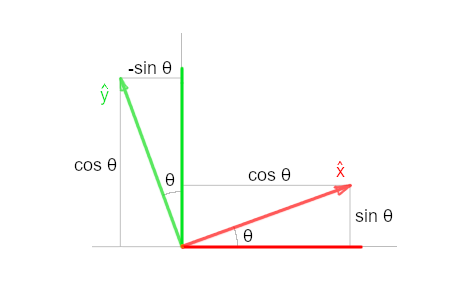
Rotation

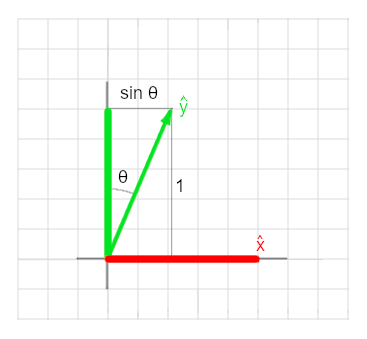
Counter-clockwise rotation by an angle \(\theta\) is developed using unit vectors established by this angle:

\begin{equation*} \hat{x}=\begin{bmatrix}\cos{\theta}&\sin{\theta}\end{bmatrix} \end{equation*}

\begin{equation*} \hat{y}=\begin{bmatrix}-\sin{\theta}&\cos{\theta}\end{bmatrix} \end{equation*}

\begin{equation*} M_{rotate}=\begin{bmatrix}\cos{\theta}&-\sin{\theta}\\\sin{\theta}&\cos{\theta}\end{bmatrix} \end{equation*}

Scale

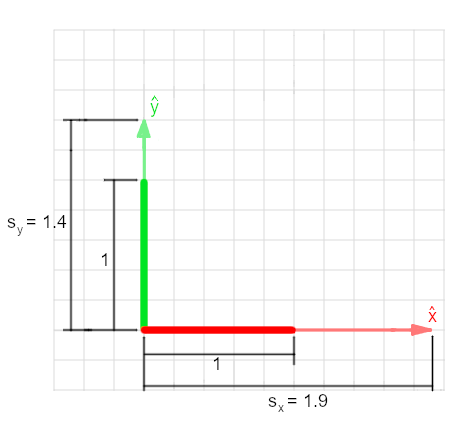
With scaling, the global unit vectors maintain the same orientation but are scaled in length by a scale factor, \(s\). The new basis vectors are then the following:

\begin{equation*} \hat{x}=\begin{bmatrix}s_x&1\end{bmatrix} \end{equation*}

\begin{equation*} \hat{y}=\begin{bmatrix}1&s_y\end{bmatrix} \end{equation*}

\begin{equation*} M_{scale}=\begin{bmatrix}s_x&1\\1&s_y\end{bmatrix} \end{equation*}

Shear

Shearing along a principal axis may be derived as follows, for example when along the x-axis:

\begin{equation*} \hat{x}=\begin{bmatrix}1&0\end{bmatrix} \end{equation*}

\begin{equation*} \hat{y}=\begin{bmatrix}\sin{\theta}&1\end{bmatrix} \end{equation*}

\begin{equation*} M_{shear,x}=\begin{bmatrix}1&\sin{\theta}\\0&1\end{bmatrix} \end{equation*}

Polygon Transformation

As an example of transformation matrices, let's create and transform a generic polygon using Python and matplotlib.

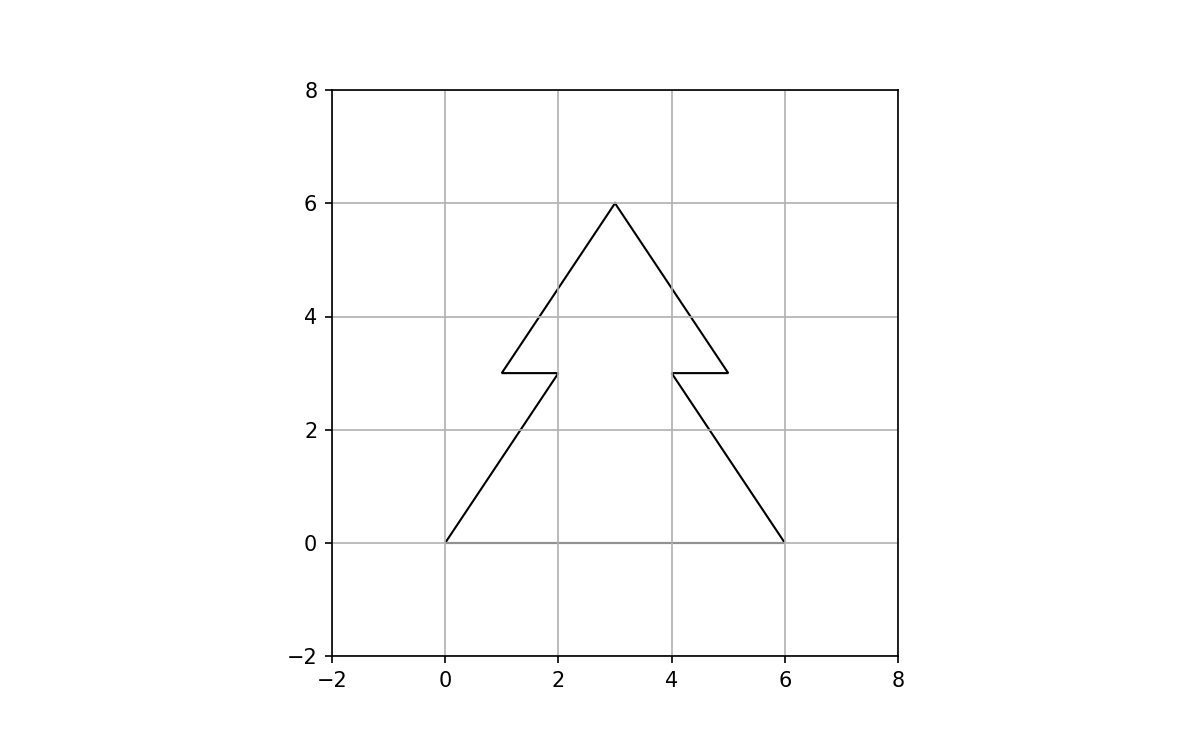
Using the following points as definition:

xy = np.array([[0,0],[2,3],[1,3],[3,6],[5,3],[4,3],[6,0]])

we obtain this polygon:

Rotation

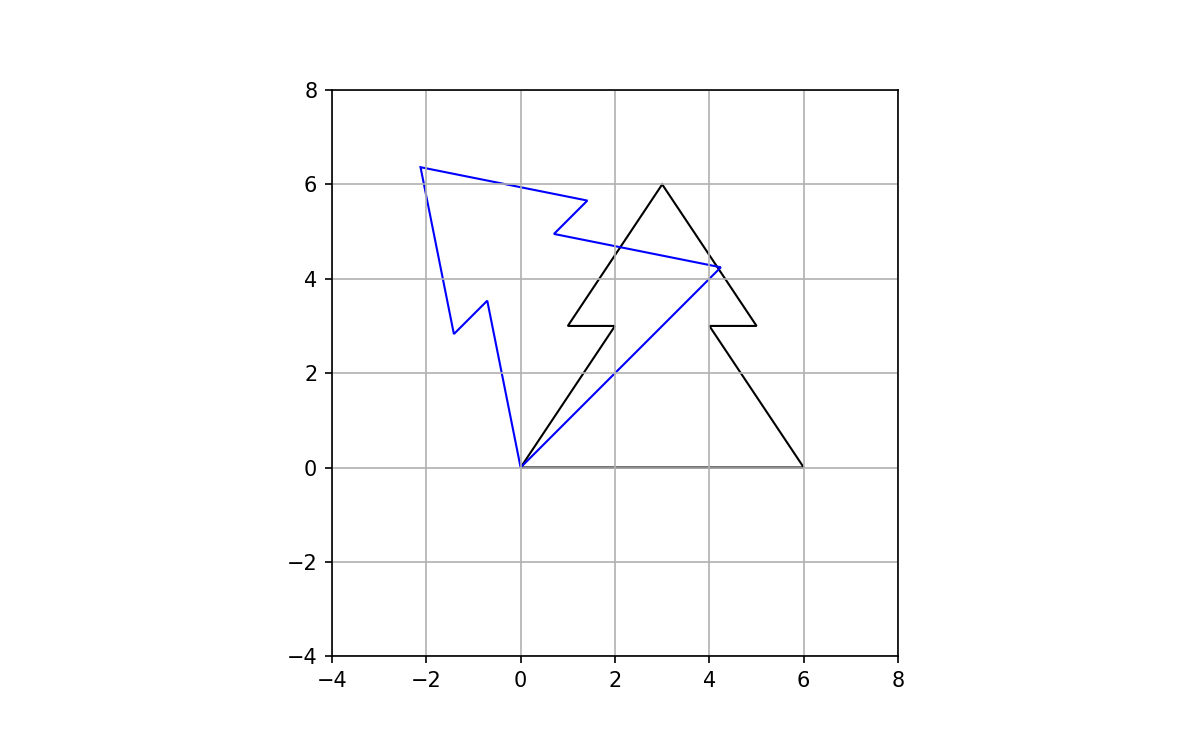
For a rotation of 45 degrees, counter-clockwise about the origin, the transformation matrix becomes:

rotation = np.radians(45)
x = np.array([  np.cos(rotation), np.sin(rotation) ])
y = np.array([ -np.sin(rotation), np.cos(rotation) ])
M = np.hstack( (x.reshape(-1,1), y.reshape(-1,1)) )

>>> print(M)
[[ 0.70710678 -0.70710678]
[ 0.70710678  0.70710678]]

The new polygon points are then calculated with:

xy_new = np.dot(M,xy.T)

Adding the rotated polygon to the plot:

Scale

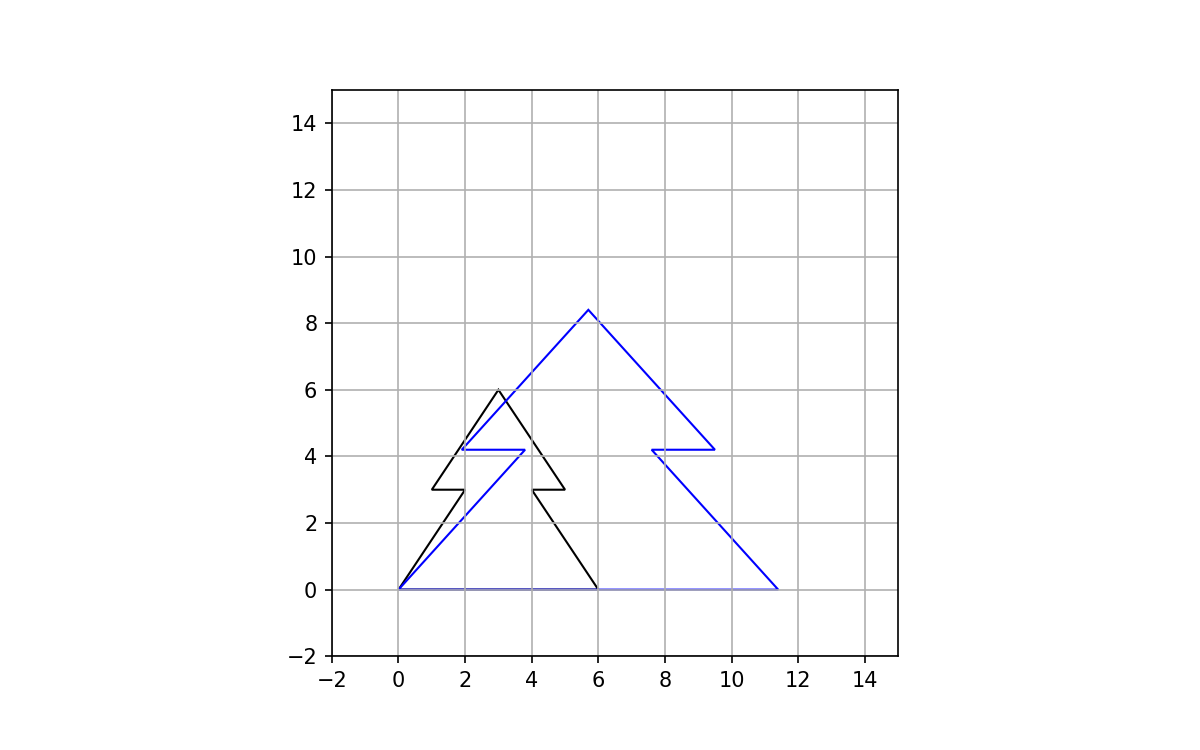
Using scale factors of 1.9 and 1.4 for the x and y axis, respectively:

sx = 1.9
sy = 1.4

x = np.array([ sx, 0 ])
y = np.array([ 0, sy ])

M = np.hstack( (x.reshape(-1,1), y.reshape(-1,1)) )

>>> print(M)
[[1.9 0. ]
[0.  1.4]]

We calculate the points for the scaled polygon the same way:

xy_new = np.dot(M,xy.T)
poly_scaled = Polygon(xy_new.T, fill=False, edgecolor='blue')

And plotting:

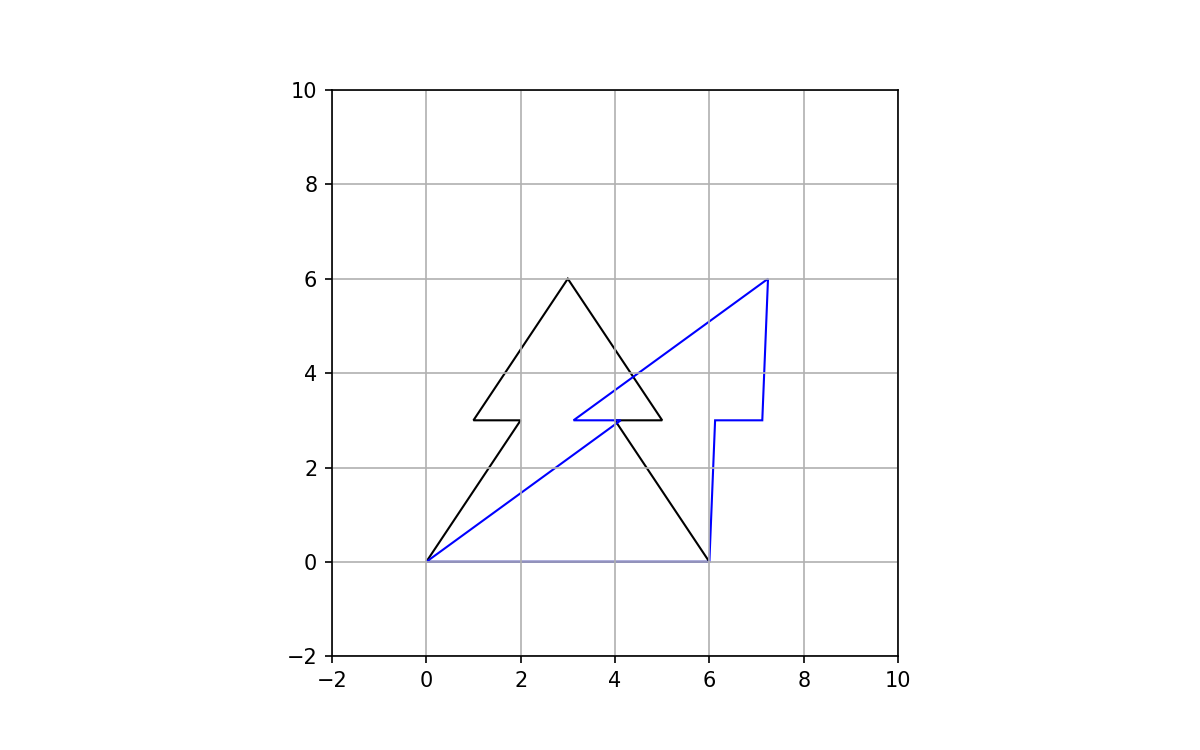
Shear

Here we will shear along the x-axis by 45 degrees. The transformation matrix is:

angle = 45

x = np.array([ 1, 0 ])
y = np.array([ np.sin(np.radians(angle)), 1 ])

M = np.hstack( (x.reshape(-1,1), y.reshape(-1,1)) )

>>> print(M)
[[1.         0.70710678]
[0.         1.        ]]

And the sheared polygon is calculated using matrix multiplication again:

xy_new = np.dot(M,xy.T)
poly_scaled = Polygon(xy_new.T, fill=False, edgecolor='blue')